Neste primeiro exemplo, será construído um modelo que busque minimizar a seguinte função f(X) = (X-8.22)². Por se tratar de um caso simples e com todos os blocos já descritos anteriormente, não será aprofundada a modelagem do problema.
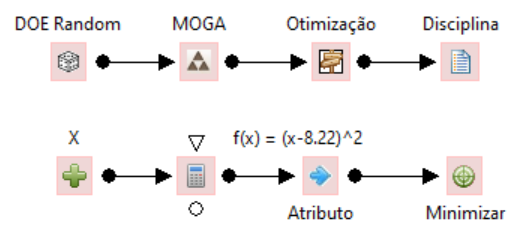
Foi escolhido um DOE Random, que cria soluções iniciais aleatórias ao problema, bem como o otimizador MOGA que é restrito a solução de problemas mono-objetivos. Por se tratar de uma função parábola com concavidade para cima, trata-se de um problema de minimização sem nenhuma restrição. Atentar-se ao fato de manter os limites da variável X dentro do intervalo correto. Quando não se sabe o intervalo deve- se estimar um possível intervalo e se o resultado da otimização estiver em um dos extremos é necessário adequar o intervalo até que o resultado esteja entre os limites.
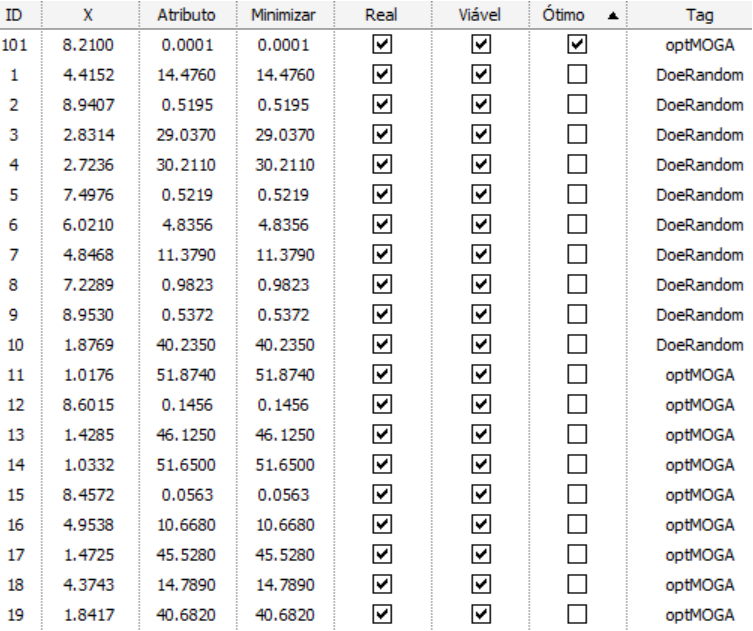
A figura acima contempla os resultados do problema. Como esperado, a solução ótima que minimize a função foi 8.2203, muito próximo de 8.2200 que seria a resposta exata. Não será abordado o erro associado a isso, pois diz respeito as definições do algoritmo de otimização, que fogem do escopo inicial do tutorial.
Alguns aspectos importantes da plotagem de resultados podem ser destacados, como a coluna “Viável” que está relacionada a aprovação ou não das restrições, bem como a “Tag”, onde é possível ver os resultados que vieram das soluções inicias randômicas, bem como os que vieram através do algoritmo de otimização. Por fim, por se tratar de um problema mono-objetivo, há apenas um valor ótimo, diferindo do exemplo tratado no próximo problema.
